
You might wonder why it does increase the FPS with Sodium(and Canvas) since Sodium has "Use Entity Culling" in its Advanced settings and enabled by default. This has been tested with other mods, Optifine(Optifabric), Canvas, and Sodium, in all cases resulting in massive fps gains in places like Game Server lobbies.
Fabric cutting optimizer mod#
This mod calculates the visibility of tile/-entities 64 blocks in each direction of the player(so a 128x128x128 cube in total), everything outside of that is considered too far away and is invisible(should somewhat line up with the vanilla "Entity Distance" setting, but future changes to this size are possible). During the rendering, the not visible ones will be skipped the same way entities behind you are. Minecraft skips rendering things that are behind you, so why is it rendering everything that you still can't see because of a wall in the way? This mod utilizes your other CPU cores/threads to do really quick path-tracing from your camera to all tile/-entities to determine rather they are visible or not. But, I don't think that this is remotely the right way to mathematically model the problem.īeen a long time since calc, if I can remember any of it, and I'd appreciate suggestions or pointers.Using async path-tracing to skip rendering Tiles/Entities that are not visible. Tentatively, this can be written as 4a + 4b + 2c + 2d + 1e <= 7, with a/b/c/d/e being coefficients of a length ranging from either 0 - 1.
Fabric cutting optimizer how to#
Math?: at this point I thought to try an equation or system of equations to solve, but I'm not sure how to craft it. Works for 16 segments, but if you were solving for 32 segments, that combination shoots toward 5 billion and above. But for a dozen or so, that number of combinations goes up to half a billion and beyond.Īlgorithm #2: more efficient way of doing this is forgetting about reordering the segments like a permutation would, and then focusing on the segment coefficients only being either 1 or a 0 - in which case the number of possible combinations to eliminate is based on bits (2 count) = number of combinations. So for 4 segments, 4! = 1 * 2 * 3 * 4 = 24 permutations. For each segment, estimate of permutations is (count)!. Problem is that this is very computationally inefficient. Ostensibly the topmost answer will be a good fit, at which point I remove the used segments and start over with available wanted segments until no further solutions can be found.
Fabric cutting optimizer full#
Weakest and most wasteful solution is using five full length rods to cut a single segment out of each, but that's very inefficient in how it uses material.Īlgorithm #1: first I wrote/tried was to generate a list of permutations of the wanted segments, then filter the list by sum remainders under 7 for each combination, and then sort by smallest remainder. In eyeballing this example, best solution is probably (4, 2, 1) and (4, 2) since it uses least amount of material rods (remainders are 0, 1 cm respectively). Problem: if you have available sticks in certain sizes (7 cm) and you need to cut them in lengths of 4, 4, 2, 2, 1 cm, what's the most efficient way to determine how to efficiently cut them? By efficient, I mean both in terms of computation and in used material. Trying to define the problem and devise a solution has been stuck in my head for a few days. I'd either like to be able to construct a system of equations, or, write an efficient algorithm to solve this - and I don't have the right mathematical / algorithm vocabulary for it.

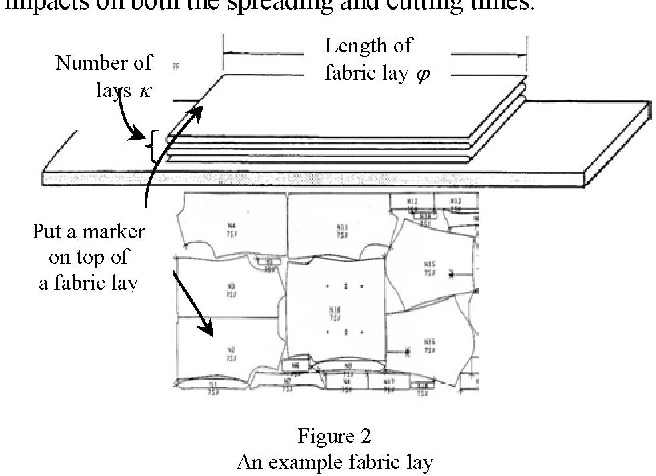

My question is somewhere between mathematical theory and algorithms, both of which I'm not very conversant in.


 0 kommentar(er)
0 kommentar(er)
